引
腾讯安全平台,最近开启了一个线上解谜游戏,题目构思很是巧妙,像个套娃一样,先给出一段代码 每打开一层,里面还有一层,一直指向最终的第八关。玩过的小伙伴们也是深陷其中难以自拔。凑个 热闹我也试着解了一下第八关。应该说这一关设计的比较巧妙,所以这里 简单整理一下解题思路,供小伙伴们自行参阅。
原题目链接: «一道即将尘封十几年的封印,不来尝试解开吗?»
原题描述
将第七关的密码输入后,将会看到第八关的关卡题目,如下图所示:
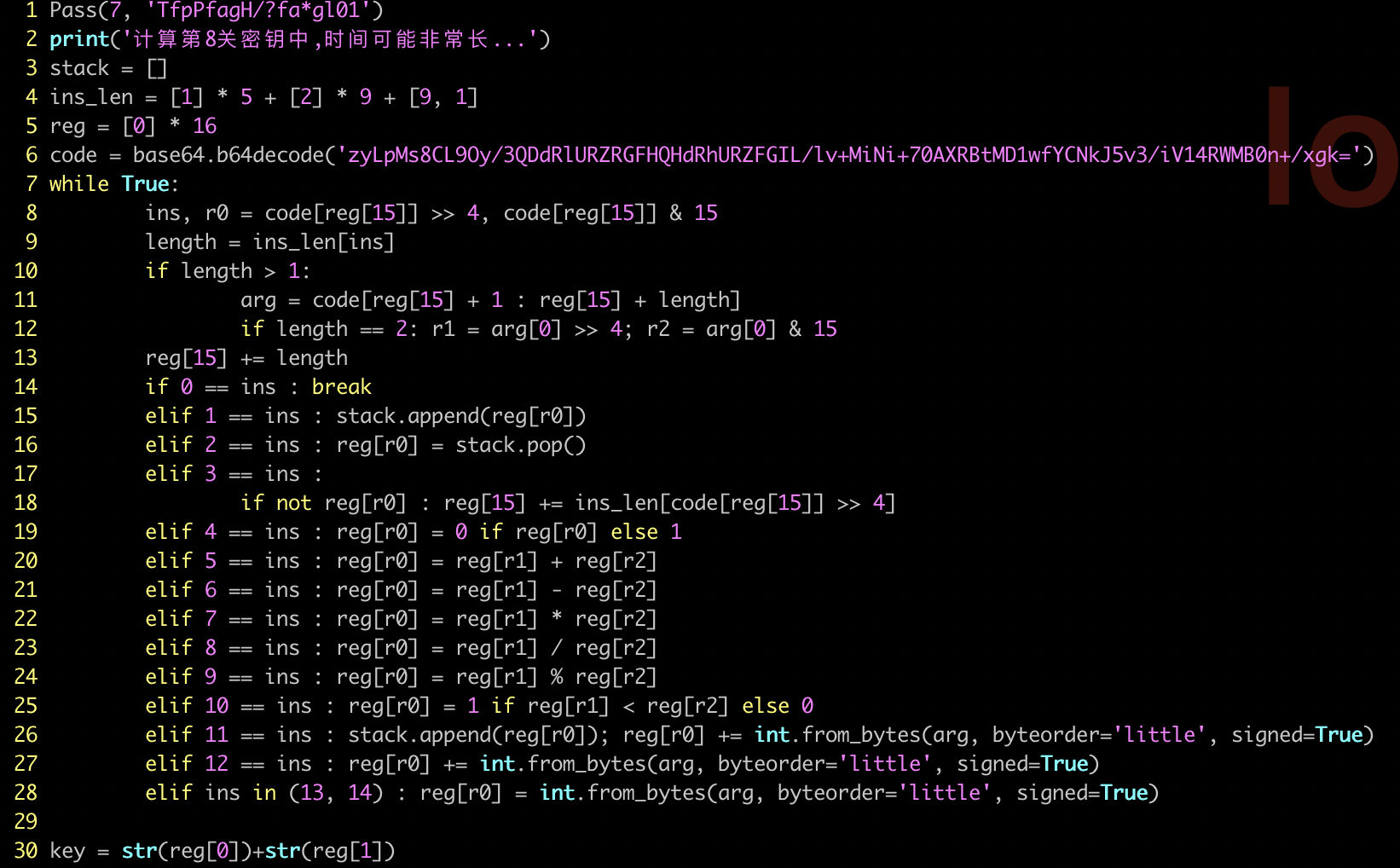
其中,第 2 行代码,给了一个提示,“时间可能非常长…”,这表明本题核心其实是一个 代码/算法优化类题目。
随后,3-6 行代码分别代表虚拟机的“栈/指令长度/寄存器/代码”等结构,
再后,7-28 行实现了一套简易的虚拟机系统;
最后,第30行,为通关密码的结果。
综上,题目中其实是构造了一个轻巧的虚拟机,麻雀虽小却五脏俱全。它包含16个寄存器, 15种指令码,加/减/乘/除/取余/入栈/出栈/循环/跳转,各类型指令具在。
不难看出命题人真是花了很多心思在里面,这样用心的 题目值得我花时间探究一下。事实也证明,我在通关后仍然意犹未尽,这样的 感觉已经很久没有过了,畅快。
题意分析
通读虚拟机代码,不难发现,本题目的几个核心的点:
- 一个本意考察算法优化的题目,题面却是个虚拟机;
- 第6行的 code 为虚拟机实际执行的代码指令;
- reg[15] 为指令寄存器,相当于 X86 架构下的 EIP 寄存器。
综合分析以上三点,要解决这个问题,大概分两步:
- 伪代码还原(俗语说的:逆向分析)
- 代码/算法优化
巧的是,这两项,都踩在了我的感兴趣点上,所以,我应该解决它。
解题
伪代码还原
伪代码还原,对我来说还原代码并不难,只是有点花精力, 只要抓住,reg[15] 是指令寄存器,code 为虚拟代码,再配合上阅读每一条 if-else 语句, 相信任何人都能够轻松解决 code 内容到伪代码的还原。还原后的伪代码如下图所示:
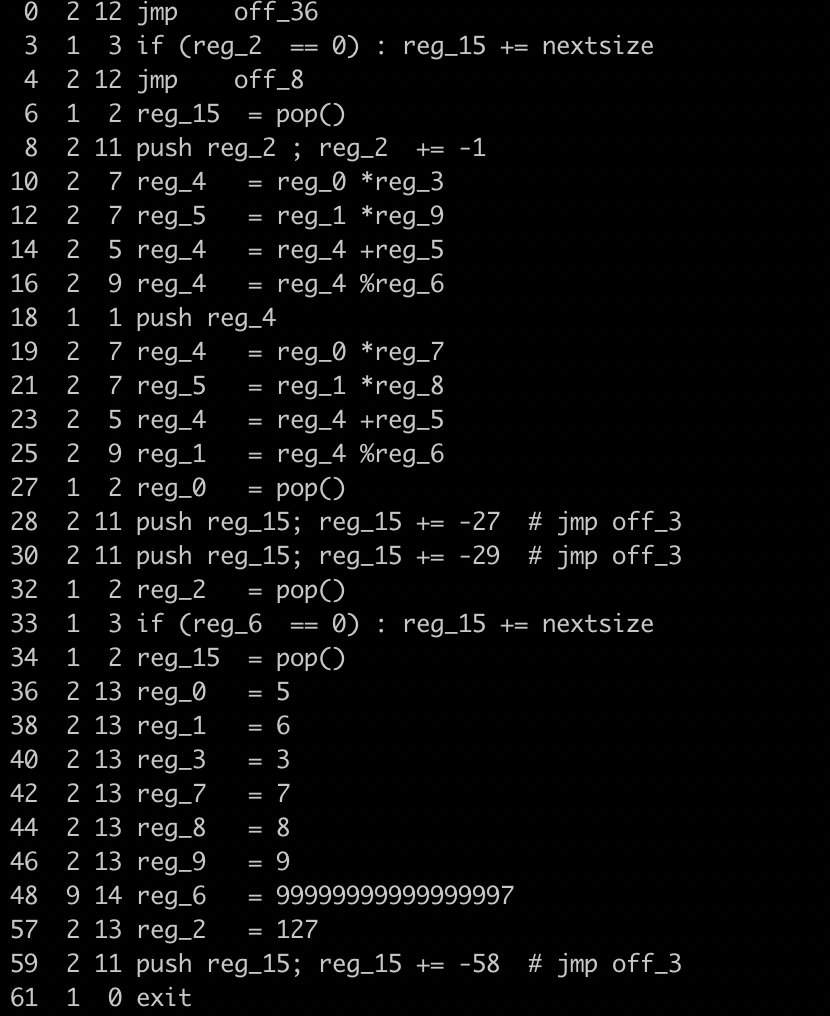
其中每一行内容中:
第一列: 代码在 code 中的偏移,可近似理解为指令地址;
第二列: 指令长度,这是依据指令码 ins 在 ins_len 中查询到的结果;
第三列: 指令码 ins ;
其他 : 是指令的伪代码。
仔细阅读这段代码,不难发现,10-27 的伪代码其实是一个循环代码段,对应的 循环寄存器是 reg_2,其初始化代码的地址为 off-57 。这段循环,在代码中表现为一个二层循环, 分别由,28 和 30 地址的代码控制跳回。而每次外层循环,都会将 reg_2 压栈,也就是说: 这是个 O(n^2) 复杂度的代码,循环的代码段将执行至少 n^2 次(具体执行多少次我也懒得 算了,总之这段代码如果要执行完,大概得执行个几天几夜才能出结果吧)。
要想快速算出通关 key 值,不做优化是不行的。但优化之前,得先把它转化成一段 逻辑清晰的代码才能理清逻辑。所以,我把这段代码又做了进一步还原,如下图所示:
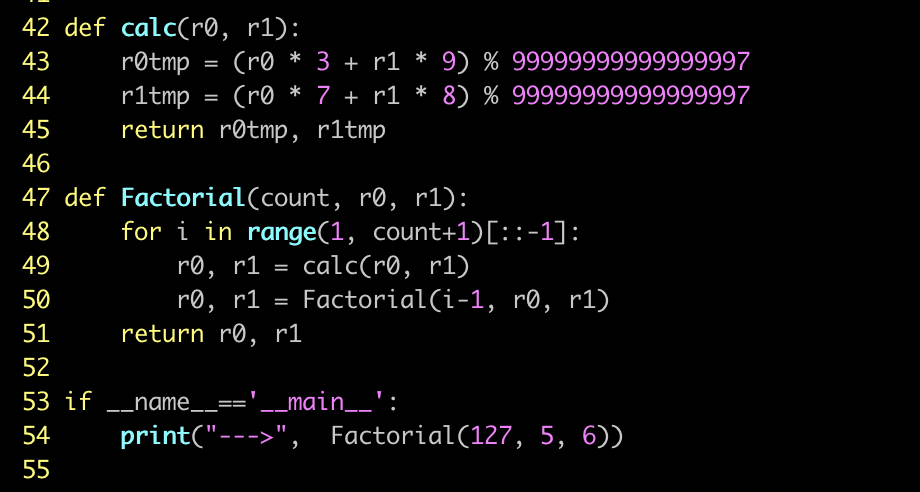
通过阅读这段代码,程序逻辑就非常清晰了。我是用递归调用 Factorial 函数的方式描述 那两层循环的。而循环代码段的具体操作在 calc 函数中。主函数中,只要将运算后的 r0 和 r1 寄存器的值,打出来,就是最终的通关 key 了。
优化分析
这段代码的优化核心在于 Factorial 函数。这是一个递归调用的函数。需要把它的时间复杂度 进行降级优化,但是它每一次递归调用都依赖前一次调用 calc 后的 r0/r1 值。也就是说, 要想优化这段代码,首先要将 calc 的逻辑进行抽象,如果能为它建立一个通项公式, 就最完美了。
继续分析 calc 的代码,不难发现,99999999999999997 这个值非常地可疑。通过搜索引擎, 我们可以迅速知道这是一个比较大的 质数(素数)。而了解过“密码学”或者学过“离散数学” 的读者都知道,质数取余这个操作,有很多奇妙的性质。 也就是说,这段代码值得挖掘。继续研究,可以得到如下的推导过程:
令:r0 为 A, r1 为 B,则,calc 函数对 (A1, B1) 可以描述为(暂时先不考虑取余操作):
A1 = 3 * A0 + 9 * B0
B1 = 7 * A0 + 8 * B0
再迭代一级后,(A2, B2) 可描述为:
A2 = 3 * ( 3 * A0 + 9 * B0 ) + 9 * ( 7 * A0 + 8 * B0 )
B2 = 7 * ( 3 * A0 + 9 * B0 ) + 8 * ( 7 * A0 + 8 * B0 )
这种非等差数列的元组,似乎不存在容易观察的通项公式。 但,这些数学式子却让我想起了“矩阵乘法”, 如果用“矩阵”描述上面的逻辑, 不难得到如下内容:
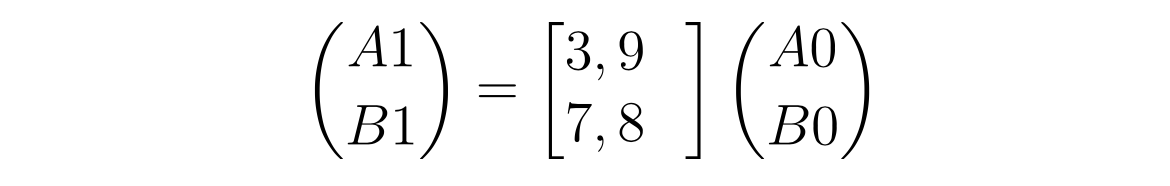
和
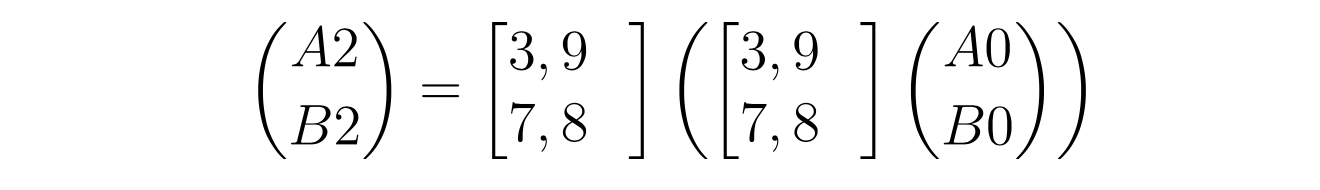
而矩阵乘法,满足结合律,所以,很容易就可以得到下面的式子:
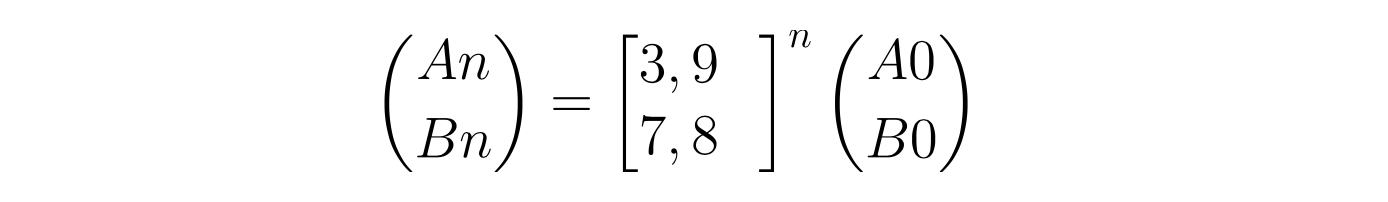
拿到这个公式,就比较完美了,它意味着:“中间所有的循环迭代,本质上都只是对前面系数矩阵的 乘法操作,当需要运算最终结果时,再把 (A0, B0) 带入到上面的式子,就能一步求出 (An, Bn)。
这时,不要忘记前面忽略的“素数取余”操作,但是,我们知道素数取余这个操作满足分配律:
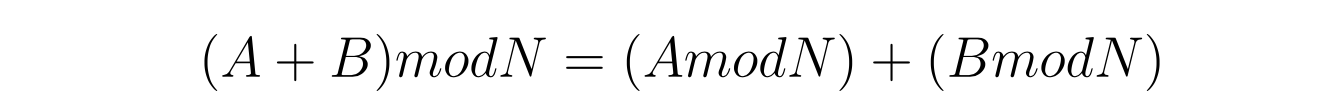
也就是说,我可以把取余这个操作,分配到每一次运算的过程之中。它和矩阵运算的逻辑完全不冲突。
至此,优化分析的过程完成。对这段代码优化的任务完全可解。
代码/算法优化
拿到了 calc 的通项公式后,下一步就是大刀阔斧的改造 Factorial 函数了,基于通项公式, 我们知道,Factorial 函数的本质是系数矩阵的乘法,我们只要拿到通项公式中的 n 值, 就可以算出最终结果,而依赖 reg_2 的初始值 127 ,所以实际的 n 值应该是 (2^127-1) 粗看一眼,这个数应该还是挺大的。于此同时矩阵幂运算对取余也没听到过什么特性。 这里就需要再进一步考虑这个问题了。
其实类似的问题,在现代密码学中会经常遇到,在实现各种密码学库的过程中, 会遇到各种指数级别的运算优化。这样的问题对于这些“密码学库”来说完全是小菜一碟。 更幸运的是,我工作之后,有一个系统学习“密码学库实现”的机会。
所以我知道,在基于“椭圆曲线”的运算中,有一个使用“倍点计算”的优化方案。 它的核心优化思路:“把某些计算(“点乘”运算)得到的中间结果保存下来, 再把它使用到最终的运算中。”。其实,这个思路就非常符合现在遇到的这个问题, 虽然通项公式中 n 这个数值本身是 2^n 级别的一个值。但我可以用保存幂级运算中间结果 的方式去追赶它,换句话说,如果我把系数矩阵中每一个 2^n 的幂次存起来,得到一个 2^n 幂次的矩阵结果表,再用这个结果表去计算最终的值,就可以非常快的算出最终结果了。 而且,在计算 2^n 这个过程中的每一次计算,其实都是前一次计算结果的倍乘,这样,我只需要循环127次, 就可以得到最终的系数矩阵结果了。这样可就完美多了。
基于这个思路,我最终完成了对这段代码的优化,虽然最终代码只有40行,但看完上面的解题过程, 应该也能知道,这几行代码的编写其实并不容易,最终代码的截图如下:
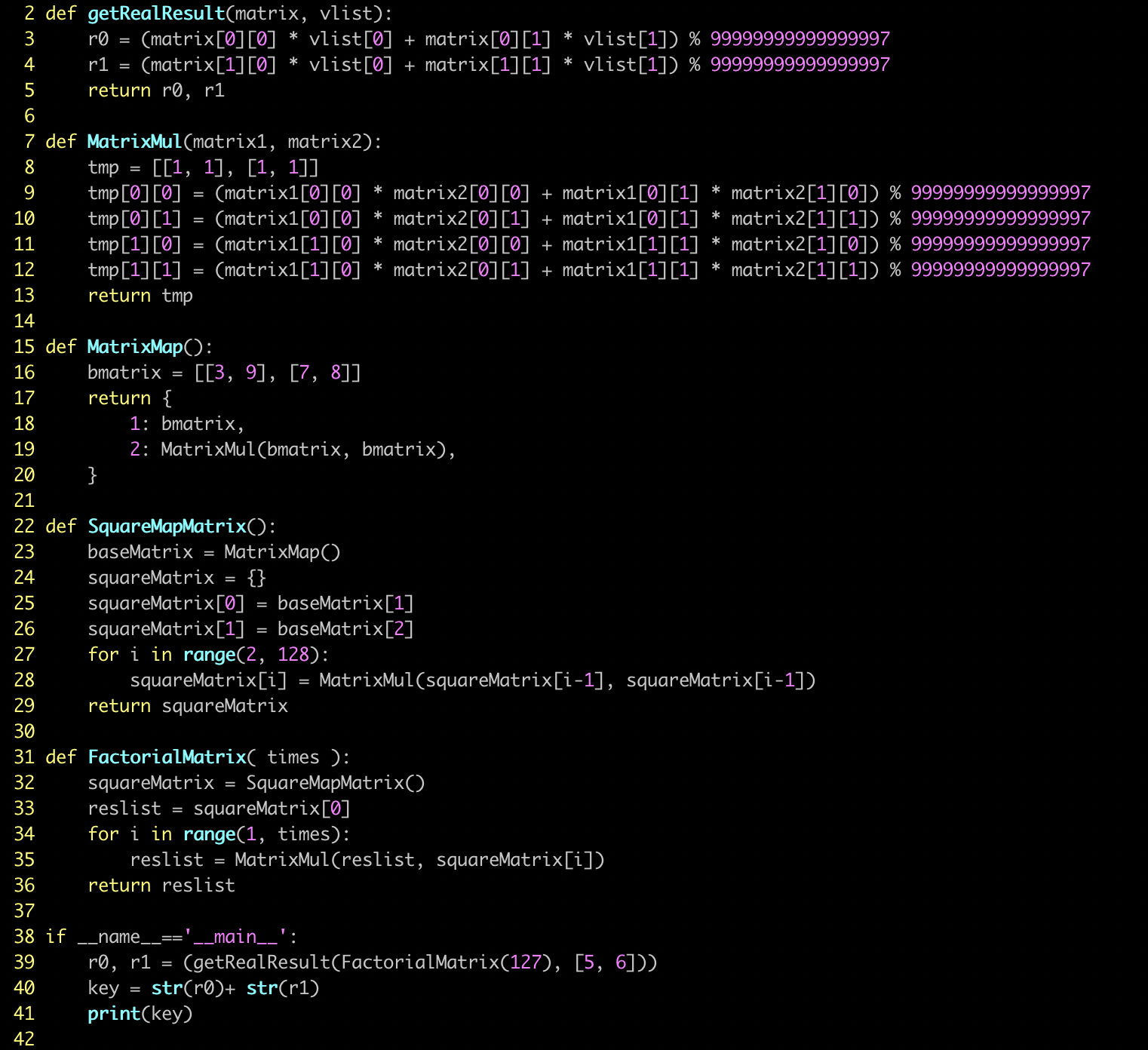
其中 getRealResult 函数,就是带入 (A0, B0) 计算出最终结果的函数。 MatrixMul 是矩阵乘法 的实现函数。MatrixMap 是计算系数矩阵乘法的函数,SqueareMapMatrix 是计算系数矩阵 2^n 次幂结果表的函数,FactorialMatrix 是优化后的 Factorial 函数,该函数依赖矩阵表,计算出 系数矩阵的最终结果。
主函数,就是用来拿到第八关最终 key 的调用过程。
总结
这里附上过程中的两个代码文件,供读者自行参阅:
虽然这是一道解谜的题目,但它的本质却是一道数学题。数学是工具,工具就是生产力。
想深入下去做技术,其实永远也离不开数学。我们每天都在使用数学推演结果带来的便利,却抱怨 学数学无用,数学会觉得冤的。




