前言
最近在读OpenSSL的命令参数,在这个学习过程中发现OpenSSL之中,架构了一个非常庞大的理论系统,结果原以为学习一两天就能学完的基础知识,整整学了两个星期,才学到一些皮毛。
之前整理了一篇证书相关的学习笔记,这篇将涉及一些OpenSSL同非对称算法(RSA、DH、DSA)之间的知识。
非对称加密算法模型
概述
非对称算法广泛应用于数字签名和密钥协商的场景下。相比普通加密算法,非对称加密算法更侧重公开性(密钥公开,算法实现公开),这个特性是由现实生活中常见的攻击手法决定的(暴力猜解,逆向分析算法实现),可以发现它解决这种问题的思路很有趣:
“你是对我感兴趣么,那我就直接就告诉你喽。”
通常情况下呢,面对这种毫无趣味的人,你都会觉得这玩意真没意思,然后就不去尝试了,它就安全了。:-)
非对称加密算法一般会有两个密钥,一个为公钥(pub_key),另一个为私钥(priv_key),两个密钥内容各不相同,其中公钥可以对众公开,而私钥不公开。同时攻击者很难通过公钥以及加解密算法反向推出私钥。事实上,加密算法E(x)同解密算法D(x) 的实现一般也不太相同。
常见算法
非对称加密算法在“密钥协商”场景下,有两种情况,一种是“密钥磋商”;另一种是“密钥交换”,在密钥交换时公钥总是用于加密数据,而私钥总是用于解密数据。而在 “数字签名”场景下,操作过程又正好相反,即“公钥用于解密(验签),而私钥用于加密(签名)”。正是这些不同,产生了下表:
| OpenSSL提供的算法 | 可用于“密钥协商” | 可用于“数字签名” |
| DSA | -- | 可以 |
| DH | 可以 | -- |
| RSA | 可以 | 可以 |
看完这个表格,我觉得RSA算法真是完胜,有种男女通吃的赶脚。
常见的应用场景
数字签名
个人曾经一直觉得,“数字签名”这个名词听起来很有文艺范,它要解决的问题又很不好理解,所以一直觉得那是个特神奇的领域,绝对是“高端大气上档次”。后来发现,这玩意想要解决的,竟然是一个显而易见的哲学问题:“请快速证明,我就是我自己”。

为了更好的,理解这个哲学问题,我决定先编一个故事。
你在网上认识一个网友D,你俩聊得特Happy,但相互没见过面。有一天,有个人敲你家房门,他告诉你:他是D,他想给你个惊喜,来看看你。结果呢,你这家伙生性多疑,完全不信这话,非要核对一下身份,怎么办呢,此时你要做的事情就是证明眼前的这家伙就是D。与此同时他面临的问题就开始哲学起来了:“请快速证明,我就是我自己。”
其实按理来说这个问题并不太难,你俩只要回忆一下你们之间聊过的独特的话就可以了。
但有些时候问题确实很麻烦,比如你们俩的聊天内容总会被第三方读到(比如你家里的间谍“路由器先生”,或者他家里的间谍“交换机先生”,甚至你们聊天的会话也可能会被黑客放置了“窃听器”),这时候你们聊过的内容就不再只有你们两个知道,发现了没,哲学问题从“普通模式”转眼就变成“地狱模式”啦。

到了这里你可能很快就想到,我有身份证啊,有了身份证,我就能证明这个哲学问题了。恭喜你,你已经打通了任督二脉,没错的,身份证是每个人身份的标识,但是互联网中没有实体身份证,能有的只是一堆数字或者字符。当某一段数字或者字符具有了“身份证”属性后它就成了“数字签名”。
“数字签名”一般由“CA机构(相当于公安局的户籍管理部门)”签发,网络中每个人都只相信CA说的话,当然了CA机构自己也需要被认定。它的签名是由它自己签发的(自签名)。
密钥约定
咱们继续数字签名章节的“哲学问题”往下聊。你和朋友D那天特别开心,然后他回家了。你们还是每天在网上聊天打发时间,但是突然有一天,聊天室服务器被黑客H入侵了,他这人不坏,就是对每个人的聊天记录感兴趣(好吧,我承认,他是个喜欢偷听他人聊天的变态)。
虽然你和D的谈话被人看见也没什么(别以为我会相信),但知道有人偷窥这个事之后,心里也总觉得怪怪的。你开始思考是不是把聊天记录做个加密,以免黑客H看到。你朋友D想了想这个提议,同意了,并且夸你聪明。
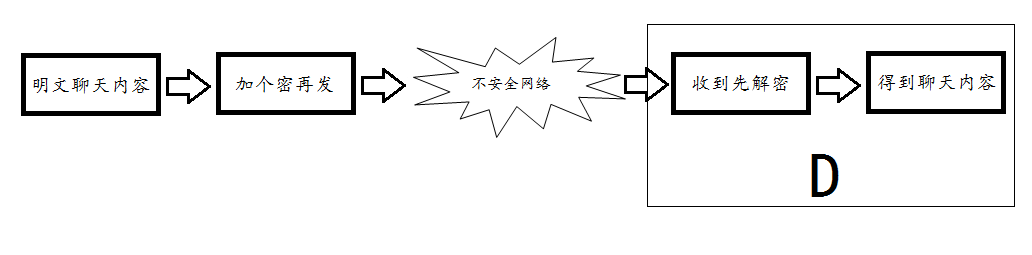
事情进展的顺利,加密算法也选好了,用上了当前性价比很高的3DES加密算法。最后的问题就是约定密钥了,这时你发现问题了,怎么把密钥告诉D而不告诉H呢,要时刻记得H是个变态,他一直研究你们的聊天记录呢。
一旦你在聊天中说出了密钥的内容,他马上就会知道,于是你们只好通过其他途径共享密钥,为了避免黑客H猜解出密码继续翻阅你们的聊天记录,你们每次开始聊天都会进行“共享密钥”的操作,如果每次交换都单独找其他通讯渠道,过于繁琐,也不易操作。
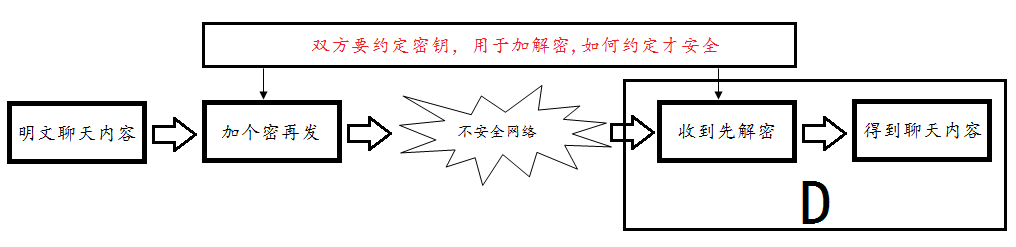
于是一大帮数学家想了两种靠谱的思路来解决“密钥约定”的问题。
思路1(密钥交换):
先假设我们要传输的密钥为 HELLO
- 首先用D的公钥D_pub_key 将密钥(HELLO)进行加密,得到密文(OLLEH)。
- 将密文(OLLEH)通过开放会话传送给D。
- D拿到密文(OLLEH)后,使用自己的私钥D_priv_key进行解密还原出密钥明文(HELLO)。
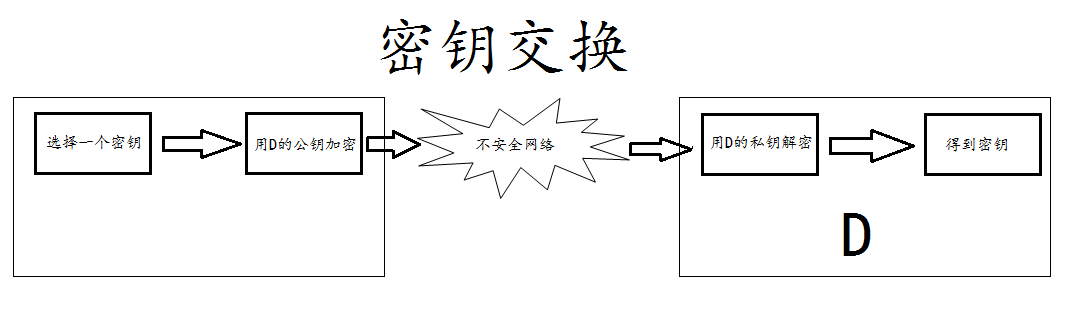
此刻密钥约定成功,即使黑客H看到了密文(OLLEH)也没关系,他没有D的私钥,自然无法解出明文的密钥。 于是你们终于可以放心的用3DES加密算法聊天了。
思路2(密钥磋商):
这个思路的精髓在于“磋商”,过程类似于买东西时候 “砍价”。具体过程描述如下:
首先呢,通讯双方各想一个密钥(两侧的密钥分别为K1、K2)记在心里,随后各自将这个密钥做一次变形(假设变形方法为E1)成为一个密钥参数(两人生成的参数分别为Z1、Z2),并把它通知对方,此时双方都能够拿到对方的密钥参数Z,用自己刚才想到的密钥K再做一次变形(假设处理方法为E2)作为最终密钥(K3)。
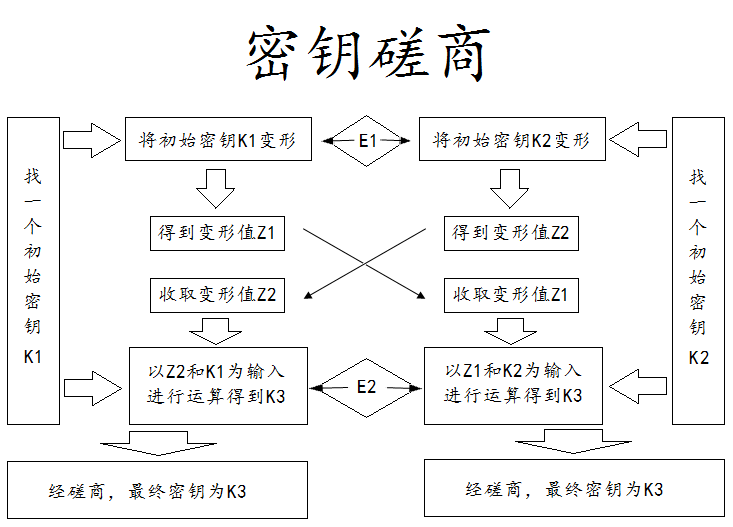
由于K3的确定过程中既有K1参与又有K2参与,所以只要算法E1和E2选择得当,双方是能够可以得到相同K3结果的。
在这个密钥约定过程中,黑客H能得到的只有通讯双方相互发送的密钥参数Z,在攻击者不知道任何一方初始密钥(K1和K2)情况下,便无法得到最终密钥K3。
于是,双方同样可以进行3DES的加密通讯了。
密钥生成
个人一直觉得说是“密钥生成”,这个说法一直不够完美,不完美的原因有二:
- 得到的密钥文件一般都是公私钥一体的文件,也就是说公私钥是成对出现在相同文件中的。
- 在DH算法结果中,其实只存在密钥参数而无密钥存在,其结果密钥是双方在API调用中,通过代码实现计算出来的。
但不管哪种情况,还是先来看看这几种非对称加密算法相关的指令格式吧。
生成DSA密钥
DSA密钥生成相对复杂,一般分两步,首先要生成一个密钥参数文件,生成指令如下:
此时dsa512.pem 文件中就存储了一组dsa密钥参数,想要查看其内容,可以使用-text选项,指令格式及执行结果如下所示:
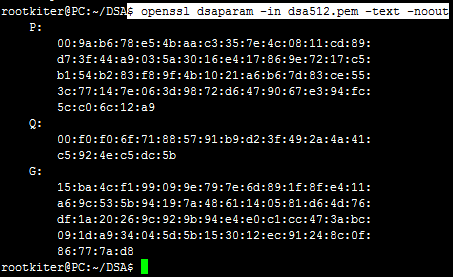
这表明密钥参数中包含了3个参数的值,分别为P、Q、G,至于这三个值具体有什么作用,是DSA算法的内容,不在本文讨论范围,只要知道它们是DSA密钥参数就足够了。
生成DSA密钥
有了DSA密钥参数后,即可根据参数生成DSA密钥了。指令格式如下:
此时生成了一个名为 dsa512_1.key 的文件,OpenSSL同样提供了查看该文件内容的指令,指令格式及执行结果如下所示:
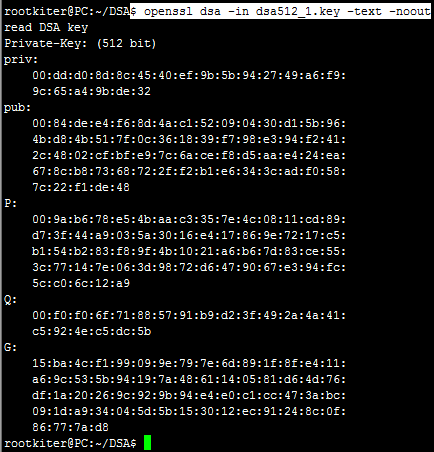
可以看到,新生成的密钥文件比之前的密钥参数文件多了两个字段,分别为priv字段和pub字段,它们分别代表这DSA私钥和公钥的主体。
细心的读者应该发现这个密钥的文件名为dsa512_1.key这么起名,有什么意义呢,下面我们再执行一遍生成密钥的操作,来生成一个dsa512_2.key这个文件,然后比对一下它和dsa512_1.key的区别:
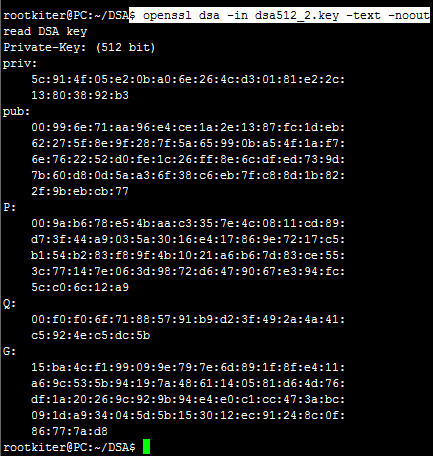
看出dsa512_1.key 和 dsa512_2.key 这两个文件的不同点了么,他们在使用了完全相同的命令和密钥参数后,却得到了完全不同的密钥对(仔细比对priv和pub的字段结果)。
不是你眼花了,也不是gendsa指令出错了,而是DSA密钥在生成过程中,会引入一个随机数作为输入,在未指定随机数时,指令会随便找一个随机数拿过来用,这就导致了每次得到的密钥对各不相同。
这个随机数也可以通过制定rand种子来设置,指令格式如下(不过经测试发现,即使制定了输入的随机数种子,生成的密钥仍然各不相同):
生成DH密钥参数
DH密钥参数生成方法非常简单,只需要一条命令:
那么生成的结果中内容有什么呢,可以用另一条命令:
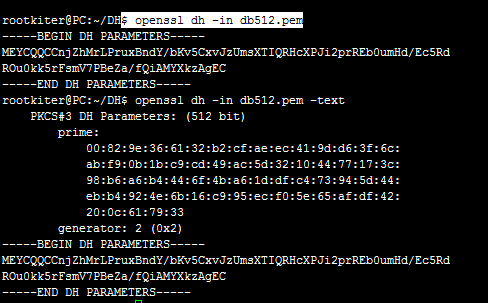
这玩意具体什么意思呢,你也别问我,我现在也还没搞懂,等搞懂了再说。
密钥协商的过程是通过调用API进行的,所以通常都需要将上面的密钥参数写到代码中,为了便于代码移植,dh指令提供了-C参数,用于C代码格式的调用(好贴心呢):
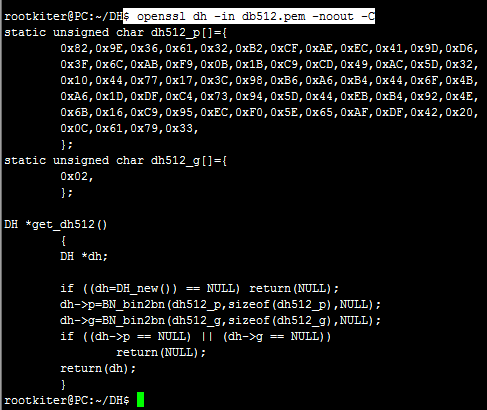
生成RSA密钥
RSA密钥生成非常简单,一行指令轻松搞定,格式如下所示:
想要查看密钥中的内容,可以使用如下指令:
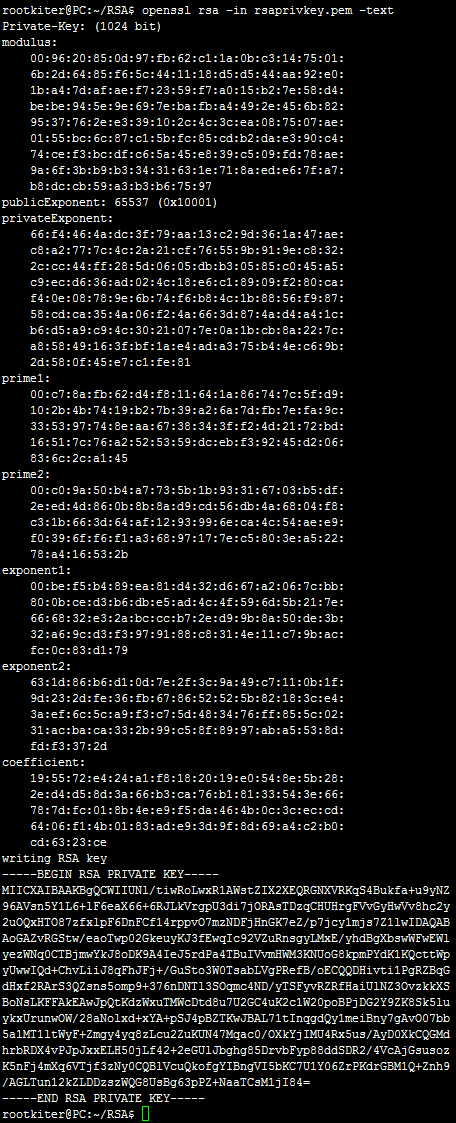
这一大堆都是什么东西呢,也是别问我,去问那帮搞密码学的数学家吧,他们会告诉你的。
公钥提取
由于DH算法无公私钥机制,所以这里提到的公钥提取,只涉及DSA公钥和RSA公钥。
提取DSA公钥
从DSA密钥文件提取DSA公钥的方法很简单,指令格式如下:
查看公钥内容:
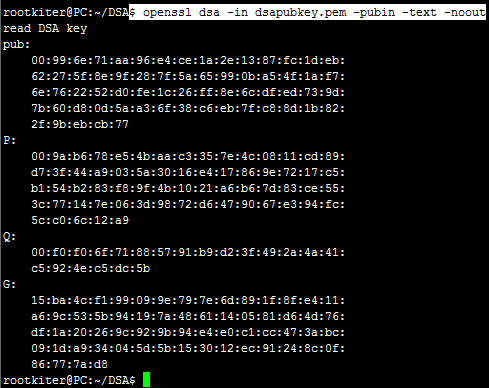
对比“生成DSA密钥”章节的截图可以发现,公钥实际上是密钥文件的一部分。
提取RSA公钥
从RSA密钥文件提取RSA公钥的方法很简单,指令格式如下:
查看公钥的内容:
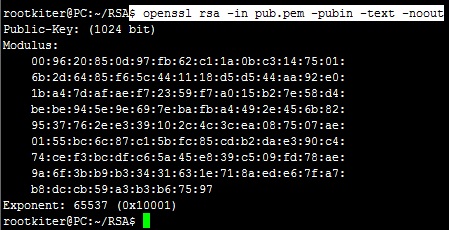
可以看到,RSA公钥同样只是密钥文件中的一部分,可以去对比下“生成RSA密钥”章节中的截图。
总结
这篇学习笔记记录了OpenSSL中和非对称加解密算法相关的一些潜在知识,并不完全,与之相关的其他内容将在下一篇学习笔记中继续完善。




